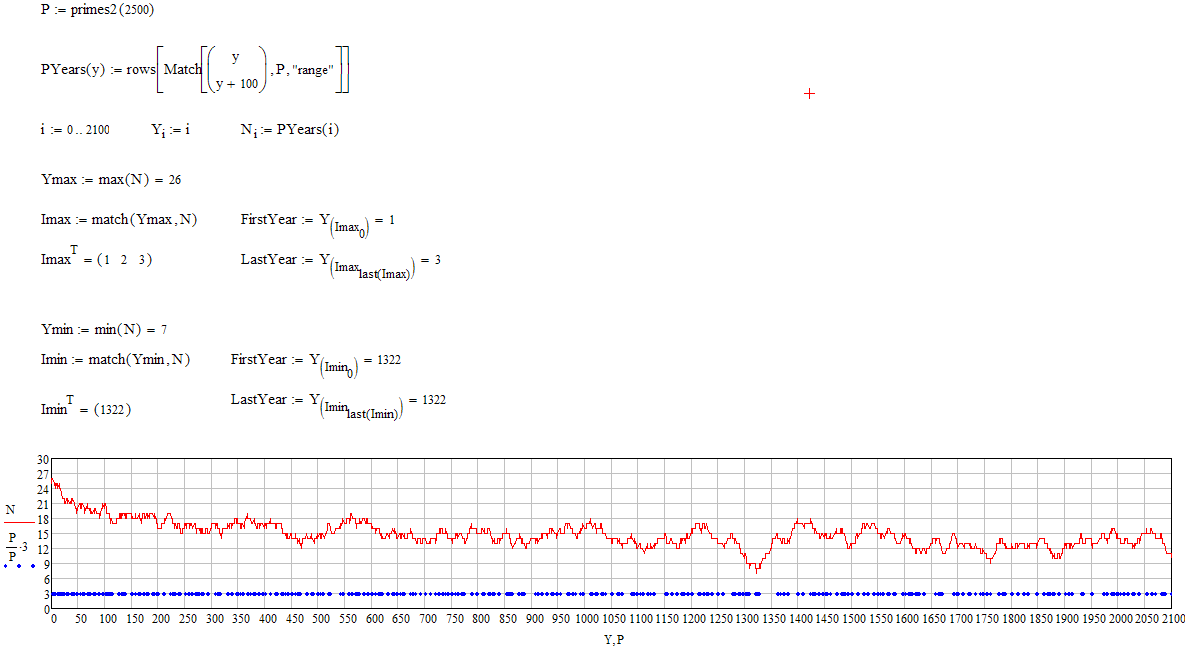
To keep it simple, well take account of the well known fact that in every year since 0 AD (0 CE), at least one mathematician has been born who lived to be 100 years old. What year was the mathematician born who lived through the greatest number of prime numbered years?
In the event of more than one birth year resulting in the same maximum number of prime years, what year was the first year such a mathematician could have been born in, and what year was the last possible year.
In the first instance, you can include any (future) mathematicians born no later than this year (2016).
Mathematicians born in the years 1, 2 or 3 (assuming the get 100 years old) have lived in 26 Prime years which is the maximum to achieve.
Programming Challenge – Most Prime Mathematician!
Given the higher density of prime years in the first century compared to other centuries, I would assume that the solution to your question would be someone who lived from year 2 to year 102. Year 3 to 103 would have an equal number of primes.
Programming Challenge – Most Prime Mathematician!
Modern mathematics wear pants of this fabric:
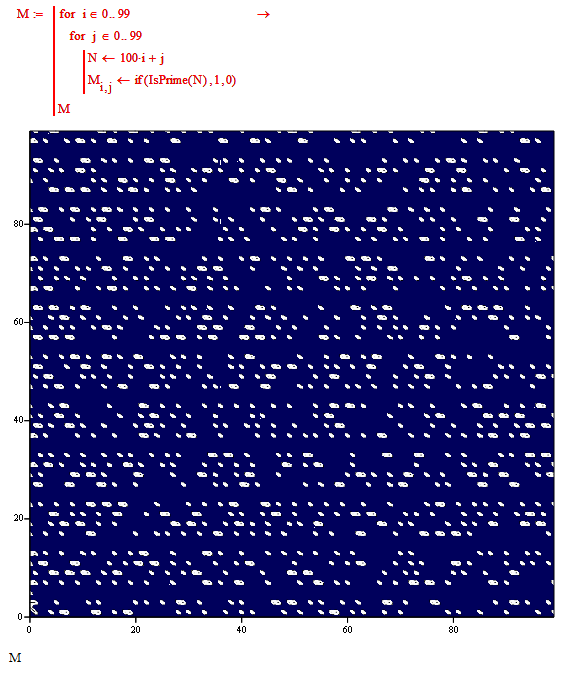
Following on from Valerys observation on Pushkin in one of the Euler Problems (Re: Programming Challenge – Project Euler – Problem 10), I wondered which mathematician (whatever) lived through the greatest number of prime years, and this suggested an immediate challenge.
You may assume in the second instance that the end date for the challenge is this year (2016), so any mathematician born this year cannot have lived through any primes.
____________________________________ If you experience problems when attaching a Mathcad sheet file ( .mcd, .xmcd or .mcdx) to the message then zip it first. To get the .zip file, use Windows Explorer, select the sheet file, right-mouse click and select Send to then Compressed (zipped) folder. This results in a .zip file containing the worksheet that you can attach
Additional challenge: What is the first year with 0 Prime years within the next 100 years?
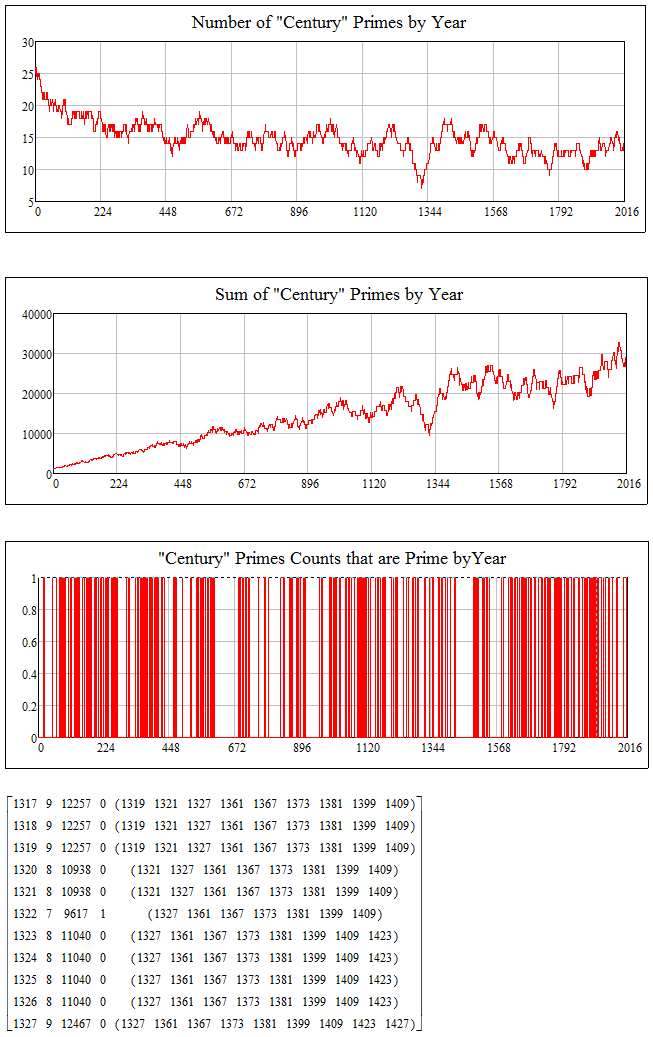
Indeed, the lowest numbered years do have the most primes in their centuries. Theres an interesting dip at 1322 though …
Indeed, the lowest numbered years do have the most primes in their centuries. Theres an interesting dip at 1322 though …
Extra imaginary points for determining the first year tha has fewer primes than 1322 ….
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Extra imaginary points for determining the first year tha has fewer primes than 1322 ….
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Programming Challenge – Most Prime Mathematician!
Maybe its better to ask for the minimum number. The solution is unique – Year 1322 with just 7 Prime years in the following 100 years.



