is nothing but the difference between M with its nearest power of 2 M )
All articles with unsourced statements
RLGR Entropy Encoding, Microsoft MS-RDPRFX Open Specification, RemoteFX codec for Remote Desktop Protocol.
is power of 2, code remainder as binary format. So
FLAC documentation: format overview
TheRun-Length Golomb-Rice (RLGR)adaptive version of Golomb-Rice coding, mentioned above, is used for encoding screen content in virtual machines in theRemoteFXcomponent of the Microsoft Remote Desktop Protocol.
S. Bttcher, C. L. A. Clarke, and G. V. rmation Retrieval: Implementing and Evaluating Search Engines. MIT Press, Cambridge MA, 2010.
Note below that this is the RiceGolomb encoding, where the remainder code uses simple truncated binary encoding, also named Rice coding (other varying-length binary encodings, like arithmetic or Huffman encodings, are possible for the remainder codes, if the statistic distribution of remainder codes is not flat, and notably when not all possible remainders after the division are used). In this algorithm, if theMparameter is a power of 2, it becomes equivalent to the simpler Rice encoding.
web pagewith a short worked out example of Golomb coding and decoding.
David Salomon. Data Compression,ISBN0-387-95045-1.
In those results, the Rice coding may create very long sequences of one-bits for the quotient; for practical reasons, it is often necessary to limit the total run-length of one-bits, so a modified version of the RiceGolomb encoding consists of replacing the long string of one-bits by encoding its length with a recursive RiceGolomb encoding; this requires reserving some values in addition to the initial divisorkto allow the necessary distinction.
Rice was motivated to propose this simpler subset due to the fact that geometric distributions are often varying with time, not precisely known, or both, so selecting the seemingly optimal code might not be very advantageous.
Articles with unsourced statements from December 2008
IEEE Transactions on Communications
Rice coding(invented byRobert F. Rice) denotes using a subset of the family of Golomb codes to produce a simpler (but possibly suboptimal) prefix code. Rice used this set of codes in anadaptive codingscheme; Rice coding can refer either to that adaptive scheme or to using that subset of Golomb codes. Whereas a Golomb code has a tunable parameter that can be any positive integer value, Rice codes are those in which the tunable parameter is a power of two. This makes Rice codes convenient for use on a computer since multiplication and division by 2 can be implemented more efficiently inbinary arithmetic.
IEEE Transactions on Information Theory
Witten, Ian Moffat, Alistair Bell, Timothy. Managing Gigabytes: Compressing and Indexing Documents and Images. Second Edition. Morgan Kaufmann Publishers, San Francisco CA. 1999ISBN1-55860-570-3
This page was last edited on 4 February 2018, at 13:51.
(9): 889897.doi10.1109/TCOM.1971.1090789.
Text is available under the; additional terms may apply. By using this site, you agree to theTerms of UseandPrivacy Policy. Wikipedia® is a registered trademark of theWikimedia Foundation, Inc., a non-profit organization.
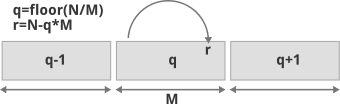
GolombRice codes can be thought of as codes that indicate a number by the position of thebin(q), and theoffsetwithin the bin (r). The above figure shows the positionqand offsetrfor the encoding of integerNusing GolombRice parameterM.
H. S. Malvar,Adaptive run-length/Golomb-Rice encoding of quantized generalized Gaussian sources with unknown statistics, Proc. Data Compression Conference, 2006.
The Code format: Quotient CodeRemainder Code, where
\displaystyle b=\lceil \log _2(M)\rceil
When a probability distribution for integers is not known, then the optimal parameter for a Golomb-Rice encoder cannot be determined. Thus, in many applications, a two-pass approach is used: first, the block of data is scanned to estimate a probability density function (PDF) for the data. The Golomb-Rice parameter is then determined from that estimated PDF. A simpler variation of that approach is to assume that the PDF belongs to a parametrized family, estimate the PDF parameters from the data, and then determine compute the optimal Golomb-Rice parameter. That is the approach used in most of the applications discussed below.
Rice coding is used as theentropy encodingstage in a number of losslessimage compressionandaudio data compressionmethods.
in plain binary representation using
is alossless data compressionmethod using a family ofdata compressioncodes invented bySolomon W. Golombin the 1960s. Alphabets following ageometric distributionwill have a Golomb code as an optimalprefix code,making Golomb coding highly suitable for situations in which the occurrence of small values in the input stream is significantly more likely than large values.
For example, with a RiceGolomb encoding of parameterM= 10, the decimal number 42 would first be split intoq= 4,r= 2, and would be encoded as qcode(q),rcode(r) = qcode(4),rcode(2) = 11110,010 (you dont need to encode the separating comma in the output stream, because the 0 at the end of theqcode is enough to say whenqends andrbegins; both the qcode and rcode are self-delimited).
Rice, R. F.; Plaunt, R. (1971). Adaptive Variable-Length Coding for Efficient Compression of Spacecraft Television Data.
The GolombRice coder is used in the entropy coding stage ofRice Algorithmbasedlossless image codecs. One such experiment yields a compression ratio graph given below. See other entries in this category at the bottom of this page. In those compression, the progressive space differential data yields an alternating suite of positive and negative values around 0, which are remapped to positive-only integers (by doubling the absolute value and adding one if the input is negative), and then RiceGolomb coding is applied by varying the divisor which remains small.[citation needed]
Remainder Code (intruncated binary encoding)
Merhav, N.; Seroussi, G.; Weinberger, M.J. (2000). Coding of sources with two-sided geometric distributions and unknown parameters.
TheJPEG-LSscheme uses RiceGolomb to encode the prediction residuals.
Selecting the Golomb Parameter in Rice Coding
(Technical report).Jet Propulsion Laboratory. 42-159.
The Golomb code for this distribution is equivalent to theHuffman codefor the same probabilities, if it were possible to compute the Huffman code.
Several losslessaudio codecs, such asShorten,[4]FLAC,[5]Apple Lossless, andMPEG-4 ALS, use a Rice code after thelinear prediction step(called adaptive FIR filter in Apple Lossless). Rice coding is also used in theFELICSlossless image codec.
(2): 228230.doi10.1109/tit.1975.1055357.
Golomb, S.W. (1966)., Run-length encodings. IEEE Transactions on Information Theory, IT–12(3):399–401
IEEE Transactions on Information Theory
An alternative approach to efficiently encode integer data whose PDF is not known or is varying, is to use a backwards-adaptive encoder. TheRun-Length Golomb-Rice (RLGR)achieves that using a very simple algorithm that adjusts the Golomb-Rice parameter up or down, depending on the last encoded symbol. A decoder can follow the same rule to track the variation of the encoding parameters, so no side information needs to be transmitted, just the encoded data. Assuming a Generalized Gaussian PDF, which covers a wide range of statistics seen in data such as prediction errors or transform coefficients in multimedia codecs, the RLGR encoding algorithm can perform very well in such applications.
Numerous signal codecs use a Rice code forpredictionresidues. In predictive algorithms, such residues tend to fall into a two-sidedgeometric distribution, with small residues being more frequent than large residues, and the Rice code closely approximates the Huffman code for such a distribution without the overhead of having to transmit the Huffman table. One signal that does not match a geometric distribution is asine wave, because the differential residues create a sinusoidal signal whose values are not creating a geometric distribution (the highest and lowest residue values have similar high frequency of occurrences, only the median positive and negative residues occur less often).
Gallager, R.G.; van Voorhis, D.C. (1975). Optimal source codes for geometrically distributed integer alphabets.
R. F. Rice (1979),, Some Practical Universal Noiseless Coding Techniques, Jet Propulsion Laboratory, Pasadena, California, JPL Publication 7922, Mar. 1979.



